Angular Margin 在人脸识别中的应用

从Loss函数的变化看人脸识别算法的进展

本文结构

Softmax

最开始大家做人脸识别还是用分类的思想，也就是把每一个人当做一类，把人脸识别看做多分类问题，于是很自然的用 Softmax Loss 来监督网络参数的训练。

但人脸识别并不是简单的多分类问题，因为不可能将每个人当做一类来进行分类，直觉上这是最完美的，但实际上并不可行，毕竟人脸的种类有无穷多种，只有在一种极端情况下，Softmax 的完美才能体现出来，即训练数据包含全世界所有人的图片，同时每个人有足够多的图片。但这种情况显然太过理想，因此在有限的训练数据集上直接使用Softmax Loss 的局限性很大，只可能在 Closed-set 的识别中取得比较好的结果。

那么面对最普遍的 Open-set 人脸识别问题，我们需要将思路从 多分类 转变到 特征提取 上来。也就是说我们要在有限的特征维度中表达出所有的人脸，同时在这一特征空间中满足不同人的人脸之间的距离尽可能大（类间距离 inter-class distance），同一人的人脸之间的距离尽可能小（类内距离 intra-class distance）。

但因为人脸作为非刚性物体的自有特征，同一人的人脸存在一定程度上的变形（最简单的就是各种表情），而不同人的人脸之间也存在一定的相似性（例如人脸都有2个眼睛1个鼻子1个嘴巴，形状都是类似椭圆形），因此很有可能会出现最小的类间距离会大于最大的类内距离，这就会造成分类错误。

Triplet Loss

为了解决上述的问题，一个重要的思路就是在训练神经网络的过程中，以最大化类间距离同时最小化类内距离作为优化的目标，这种思路直接催生了Triplet Loss。

Triplet Loss 的提出主要是两篇文章：VGG 的 Deep Face Recognition 以及 Google 的 FaceNet。

Triplet Loss在训练过程中会寻找相对于样本 A 的正例 P 和反例 N，也就是与 A 同属于一人的样本，以及同 A 不属于同一人的样本 N，并利用这三者来计算其Loss，Loss的形式大概为

$$ Loss_{triplet} = max\{ 0, distance(a, p) + margin - distance(a, n)\} $$

也就是说当a，p间距离比a，n间距离减去margin还小的话，我们认为分类正确，此时Loss的值为0，否则a，p间距离越大，a，n间距离越小，Loss值就越大。Triplet计算距离使用的是L2距离，也就是欧氏距离，在后面我们会逐渐看到 L2 欧式距离和 Cosine 距离的选择和比较。

Triplet Loss 的训练的优化目标是一个特征提取层，这一层连在网络的基础结构之后，图片经过整个网络的运算到这一层输出之后，得到一个向量，就是图片的特征向量。使用这个特征向量来计算上述的Loss值，再根据Loss值进行优化。这种方法也被称为 Embedding Learning，这一个特征提取层也被称为 Embedding 层，意思是说经过这层的处理特征被嵌入了欧氏空间进行表达，类似的方法在后续的人脸识别算法中非常常见，因为这是用特征提取方法解决人脸识别问题的一个重要途径。

这两篇文章中 Triplet Loss 的思想基本上是相同的，不同之处在于对 A、P、N 三元样本组的选取方式不同，VGG 的文章中是离线选取的，而 Google 的方法是在线选取的。从逻辑上来讲 Google 的方法更加合理一点，之后的研究工作在使用 Triplet Loss 的时候一般使用的也是这种在线选取方式。这里就存在一个坑，可以说是大坑，那就是正确的选取有效的 Triplet 三元组进行训练，一开始可能会想，这有什么困难的，随便找一个样本作为 A，他自己的其他图片不就是 P，其他人的图片不就是 N 吗？然而事情并没有这么简单。事实上满足条件的 A、P、N 三元组是非常多的，但是其中很多都是很容易就满足了上述Loss的需求，于是这些三元组对于 Embedding 层的参数优化就没有贡献作用，只有那些分类起来比较困难的三元组才能发挥 Embedding 层的作用，具体来说只有满足

$$distance(a, p)+margin>distance(a, n)$$

的三元组才对 Embedding 层的优化有意义，这种思想算是一种 Hard Example Mining 的方法。同时还有一个隐含的条件要满足

$$distance(a, p)<distance(a, n)$$

如果不满足这个条件的话，会导致训练难度非常大，因为这种三元组太过 “Hard”。
总的来说 Triplet Loss 的思想简洁直接，但没有考虑到训练数据分布情况。

Center Loss

paper and code
Center Loss 的思路主要在于尽量缩小类内距离，这也很好理解，如果所有的训练样本都能正确分类的话，那么此时类内距离都很小，相对应的类间距离也就大了。

那么如何控制类内距离呢？作者的方法是在每一个 mini batch 里，用

$$
L_C=\frac{1}{2} \sum_{1}^{m} \left \| x_i - c_{y_{i}} \right \|^2
$$

来表达类内距离，其中 $x_i $是一个样本，$c_{y_{i}} $是类中心。注意，只有当 $x_i $和 $c_{y_{i}} $属于同一类的时候才会更新这个Loss。可以看出 Center Loss 也是使用欧氏距离进行度量。
整个网络的 Loss 函数如下：

$$
L=L_S + L_C=-\sum_{i=1}^{m}log\frac{e^{W^T_{y_i}x_i+b_{y_i}}}{\sum^n_{j=1}e^{W^T_jx_i+b_j}}+\frac{\lambda}{2}\sum^m_{i=1}\left \| x_i-c_{y_i} \right \|^2_2
$$

可以看出来上式是将 Softmax Loss 和 Center Loss 结合起来的总体 Loss。
Center Loss 这篇文章还有一个贡献就是首次用可视化的形式将特征展示出来

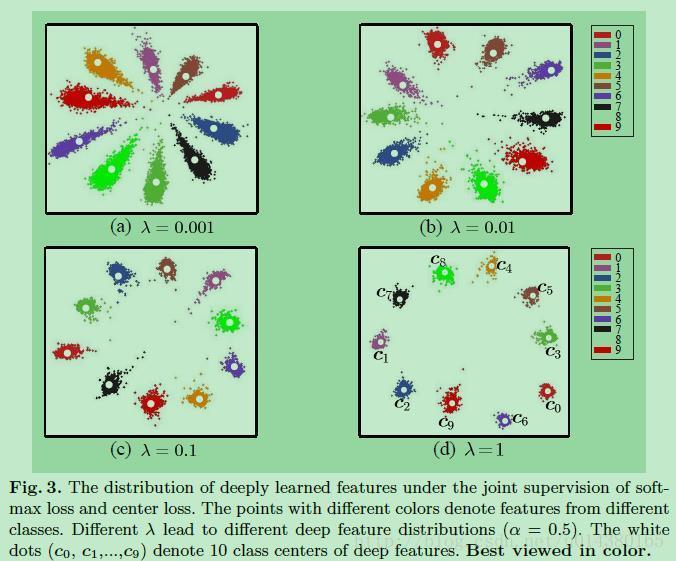
Center Loss的特征可视化

之后的很多文章都会将特征用类似的方式进行可视化，不得不说这种形式非常直观形象。

Angular Margin Loss

Angular Margin Loss 是如下一系列 Loss 函数的统称。

Sphereface: paper and code

Large margin softmax: paper and code

Additive margin softmax: paper and code

CosFace: paper

ArcFace/InsightFace: paper and code

NormFace: paper and code

L2-Softmax: paper

von Mises-Fisher Mixture Model: paper

COCO loss: paper and code

Angular Triplet Loss: code

经过这些工作，人脸识别的问题逐渐发展到现在效果最好的采用 Cosine 距离以及角度 Margin 的思想。其中涉及到的东西非常多，我只能简略的做一下总结。

最开始的突破口是在训练过程中对 Embedding 层的特征进行归一化，也就是 Feature Normalization。例子就是 7.L2-Softmax、8.von Mises-Fisher Mixture Model 以及 9.COCO Loss, 这三者非常类似，Loss 函数甚至都是一致的。其中 COCO loss 有两个版本，恕我还没弄清楚 v2 改进了什么，主要思想是在 Center Loss 的基础上，对样本 $x_i $和类中心 $c_{y_{i}} $进行归一化；L2-Softmax 和 von Mises-Fisher Mixture Model都是对 Softmax Loss 进行了 Feature Normalization。之后的 NormFace 除了 Feature Normalization 之外还做了 Weight Normalization，但仍然使用欧式距离。

另一方面，Angular Margin 的思想开端于 2.Large margin softmax，完善于 1.Sphereface。作者 Liu weiyang 大神发现 Softmax 的分类结果自然的带有一定的角度特征

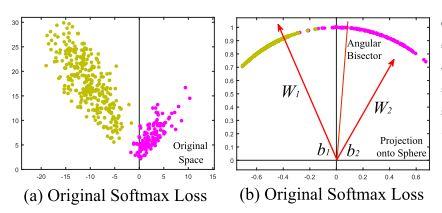
softmax-angular

于是作者对这种角度特征进行了提取，将 Softmax 的偏置项去掉，而且对 Embedding 层的输入层的参数 $W $进行归一化，从而完全用特征向量长度+特征向量同类中心夹角的方式进行表达。修改后的 Softmax Loss 如下：

$$
L_{modified}=\frac{1}{N}\sum_i-log(\frac{e^{\left \| x_i \right \|cos(\theta_{y_i,i})}}{\sum_je^{\left \| x_i \right \|cos(\theta_{j,i})}})
$$

这样处理过的特征长这样

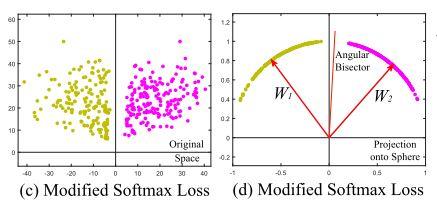
modified softmax

可以看出来经过这样的处理并没有对分类结果产生什么影响。从角度上分析，假设 $\theta_1$ 是样本 $x_i $同 $1 $类的中心 $W_1 $的夹角，$\theta_2 $是样本同 $2 $类的中心 $W_2 $的夹角，可以知道对于一个属于 $1 $类的样本，应该满足 $cos(\theta_1)>cos(\theta_2)$。

然后作者为了强化角度 Margin 的分类效果，强制要求分类过程中样本同错误类中心的夹角 $\theta_1 $要大于同正确类中心的夹角 $\theta_2 $的 $m $倍，也就是 $cos(m\theta_1)>cos(\theta_2)$。经过推导可以得出这会在 $W_1 $和 $W_2 $之间形成一个大小为 $\frac{m-1}{m+1}\theta_2^1 $的 Angular Margin，其中 $\theta_2^1 $是 $W_1 $和 $W_2 $之间的夹角。在这种情况下对上述 Loss 函数进行修改，得到 A-Softmax的公式：

$$
L_{ang}=\frac{1}{N}\sum_i-log(\frac{e^{\left \| x_i \right \|cos(m\theta_{y_i,i})}}{e^{\left \| x_i \right \|cos(m\theta_{y_i,i})}+\sum_{j\neq y_i}e^{\left \| x_i \right \|cos(\theta_{j,i})}})
$$

最终 A-Softmax Loss 的特征是这个样子的：

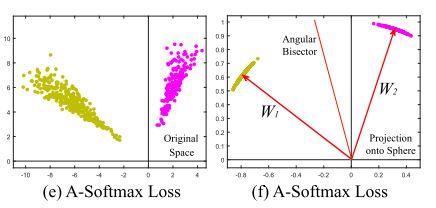
A-Softmax

可以看出分类的效果更佳明显了。

回到欧式距离和 Cosine 距离的区别这个问题上来，Embedding 到欧式空间的特征是什么样子呢？

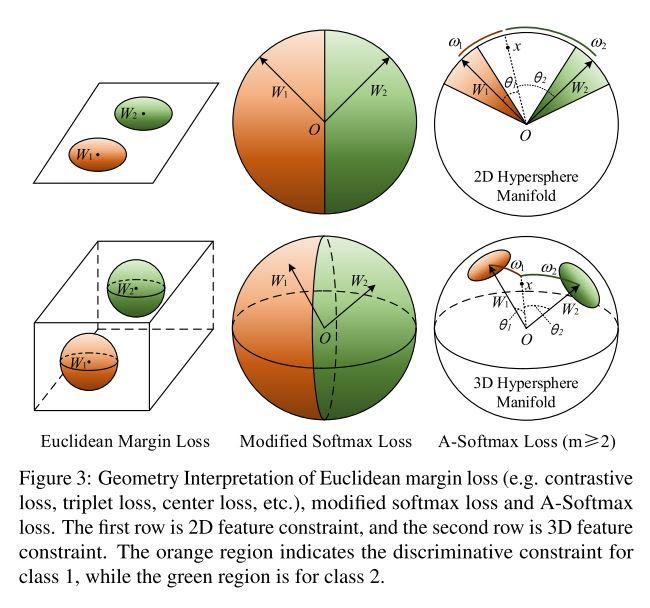
3D-interpretation

可以看到欧氏距离如何在欧式空间区分两个特征，以及欧式空间内两个类别的样本应该是如何分布；同时还可以看到 Cosine 距离所衡量的，是 Embedding 到高维流型上的特征之间的夹角，而前面所说的对 $W $进行归一化的过程，就是将所有参数映射到流型中单位球上的过程。此外作者还提出 Weight Normalization 可以在一定程度上消除训练数据中样本不均衡的问题。

Sphereface 的算法思想和数学表达都简洁而有力，实际试验效果也很不错，可以在使用较小训练数据集（小于50万张图片）的情况下，在 LFW 和 Megaface 上取得比较好的结果，在发文之时应该是 state-of-the-art 吧。而且很多试验细节都体现了作者深厚的设计和调参功底。

但是它还是存在一定的缺陷：

首先， $m $这一参数决定了类之间 Angular Margin 的大小，而当 $m=4 $甚至 $m=3 $的时候，这一约束过强，以至于训练数据中的样本很难满足这一约束，其结果就是网络参数瞬间崩溃，为了改进这一问题，作者采用了一种退火训练的方式（annealing），用一个新的参数 $\lambda $来控制 A-softmax 的强度，在训练过程中 A-Softmax 的强度从小逐渐增大，最终趋于稳定；

其次，Sphereface 在训练过程中，只对 $W $进行了归一化，而没有对 Loss 函数中的 $\left \| x_i \right \| $进行归一化，而训练过程中不同样本的 $\left \| x_i \right \| $值差别非常大，那些更像人脸的图片 $\left \| x_i \right \| $值就大，不那么像人脸的图片（例如遮挡、模糊、角度较大） $\left \| x_i \right \| $值就小，这就导致训练很容易陷入强烈的局部极值无法逃脱，因为网络参数在 Loss 的指导下只需要保证 Loss 的值尽量小，Loss 的值来源于两个方面，一是 $cos(\theta_{y_i,i})$，这是文章本来要着重表达的部分，但还有一部分 Loss 值来自于 $\left \| x_i \right \|$，也就是说网络会产生这样一种倾向：可能存在某些 $\left \| x_i \right \| $占主导的情况，在这些情况下只需要保证那些 $\left \| x_i \right \| $ 值大的样本被分类正确就可以保证 Loss 值保持在一个比较低的水准上，这就是容易陷入局部极值的问题所在。

既然发现了问题，就有改进的方法，而且还一下出来很多……

上面所说的 AM-Softmax、CosFace、InsightFace 就是从这两点上进行了改进，其中前两者的方法完全一样，和 insightface的差别也很小。

针对第一点，将参数 $m $对 Angular Margin 的控制方式从乘法修改为加法，也就是将 $cos(m\theta_1)>cos(\theta_2) $修改为 $cos(\theta_1)-m>cos(\theta_2) $（前两者）或者 $cos(\theta_1+m)>cos(\theta_2) $（后者）；

针对第二点，对 $\left \| x_i \right \| $也做了归一化，即 Feature Normalization，将其归一化到一个统一的值 $s$。

可以看出来，这些 Loss 的演进过程基本上就是在同各种归一化进行斗争，一开始的 7、8、9 三篇文章做了 Feature Normalization，但并没有讲明原因；NormFace 既做了 Weight Normalization 也做了 Feature Normalization，但还是没有阐述清楚其起作用的原理，直到最有开创性的 A-Softmax，作者为了着重表达 Softmax Loss 中样本的角度特性，将偏置项去掉，同时为了得到清晰的几何解释将 $W $归一化为 $\left \| W \right \|=1$，这其实就是在进行 Weight Normalization。

此外还有一种比较特殊的处理方法，那就是 10.Angular Triplet Loss，具体内容请见参考文章中的1和5。

其实这些归一化的操作都是有其背后的深层原因的，有一部分我已经在本文中阐述了，有的部分呢，可能需要参考其他文章。

推荐几个不错的课程：

不错的书：

Ian Goodfellow 的 Deep Learning 俗称花书
周志华老师的《机器学习》

值得 follow 的博客

其中1和2是youtube链接，需翻墙，万幸爱可可老师会在他的Bilibili主页搬运的